Background Information on DISim¶
DISim is a program that simulates Diffusion of Innovation models.
Currently at version 0.1, it replicates the experiments and results in [AR1997].
1997 Innovation Adoption Network Threshold Model¶
Refer to [AR1997] for full model details.
Original Threshold Model¶
The original threshold model did not take into account network structure. Information creating the bandwagon pressure was global; each agent had the same amount of information.
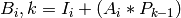
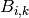 is potential adopter i’s “bandwagon assessment” of the innovation in cycle k
is potential adopter i’s “bandwagon assessment” of the innovation in cycle k
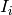 is potential adopter i‘s individual assessment of the innovation’s profitability
(given that it knows about the innovation?)
is potential adopter i‘s individual assessment of the innovation’s profitability
(given that it knows about the innovation?)
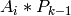 is the bandwagon pressure
is the bandwagon pressure
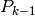 is the information that creates bandwagon pressure after k-1 cycles
is the information that creates bandwagon pressure after k-1 cycles
In fad models, 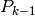 is the proportion of adopters in a collectivity
after cycle k-1 (from 1993 model [AR1993]). This is measured as the
number of adopters in the population divided by the total population.
is the proportion of adopters in a collectivity
after cycle k-1 (from 1993 model [AR1993]). This is measured as the
number of adopters in the population divided by the total population.
In learning models, 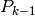 is information about profitability;
the average of information across all adopters.
is information about profitability;
the average of information across all adopters.
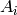 is the weight given to the information in
is the weight given to the information in 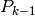 ;
how much bandwagon pressure effects agent i. The higher the
ambiguity of assessment, the more the agent is influenced by bandwagon pressure
(relies on it).
;
how much bandwagon pressure effects agent i. The higher the
ambiguity of assessment, the more the agent is influenced by bandwagon pressure
(relies on it).
If 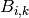 is evaluated >0, then adopt.
is evaluated >0, then adopt.
Modified Network Model¶
The 1997 modified network model does take into account network structure. In this model, profitability assessment happens on a per-agent basis and the information creating bandwagon pressure is evaluated based on the neighbors of a given agent in the network who have adopted the innovation.
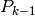 replaced with
replaced with 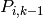
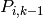 is the number of neighbors who have adopted / total population
is the number of neighbors who have adopted / total population
Max bandwagon pressure becomes # neighbors / total population
“We assume that assessed returns are normally distributed...” (p. 297).
- Trickle-down diffusion (focal to non-focal)
- Initiate by choosing 1 adopter in the focal stratum (core)
- Trickle-up diffusion (non-focal to focal)
- 1 adopter in the non-focal stratum (periphery)
“Other than the seed, for any potential adopter to adopt, it had to find out information about the innovation through the network (i.e., communicate with an adopter), and it had to find the innovation adoptable as a result of finding out this information (i.e., positive Bi, k).” ([AR1997] pp 297)
1999 Network Model Adaptation¶
Refer to [RA1999] for full model details.
(1)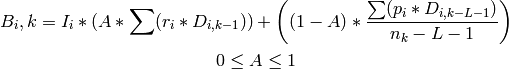
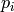 = actual profits achieved by organization i
= actual profits achieved by organization i
L = # cycles required to transmit profitability information (lag)
“Initial assessed profits and achieved profits are independently drawn from the same normal distribution” ([RA1999] p. 368)
Note
This model and simulation is not complete in the current implementation.